Optimization and Machine Learning for Safety-Critical Systems

Our research is on the design and analysis of optimization algorithms that help operate large-scale environmental/industrial systems in a safe and economic manner. The main focus has been on the electric power grid, which is currently undergoing a major paradigm-shift following the need for more resilient and secure systems, and our society’s commitment towards a carbon-free and sustainable future. This transformation of the power grid is met with many challenges: 

• The already large-scale network is growing even bigger and more fine-grained as new components and participants are added to the grid, such as electric vehicles, storage, and distributed energy sources.
• Higher penetration of renewable energy sources promotes sustainability, but it also brings more uncertainty and instability to the grid due to their intermittent characteristic. 
• On top of all these issues, the innate nature of AC power introduces nonconvexity and poses serious difficulties in finding the best decision when using classical optimization methods.
• With the rapid development of digital technology and cloud computing, more and more data are produced through sensors and human activities. Data can bring great value but also contains the risk of derailing the system if noise, gross errors, and malicious attacks are not dealt with properly.

Project 1. Enhancing network awareness with data-driven optimization and learning

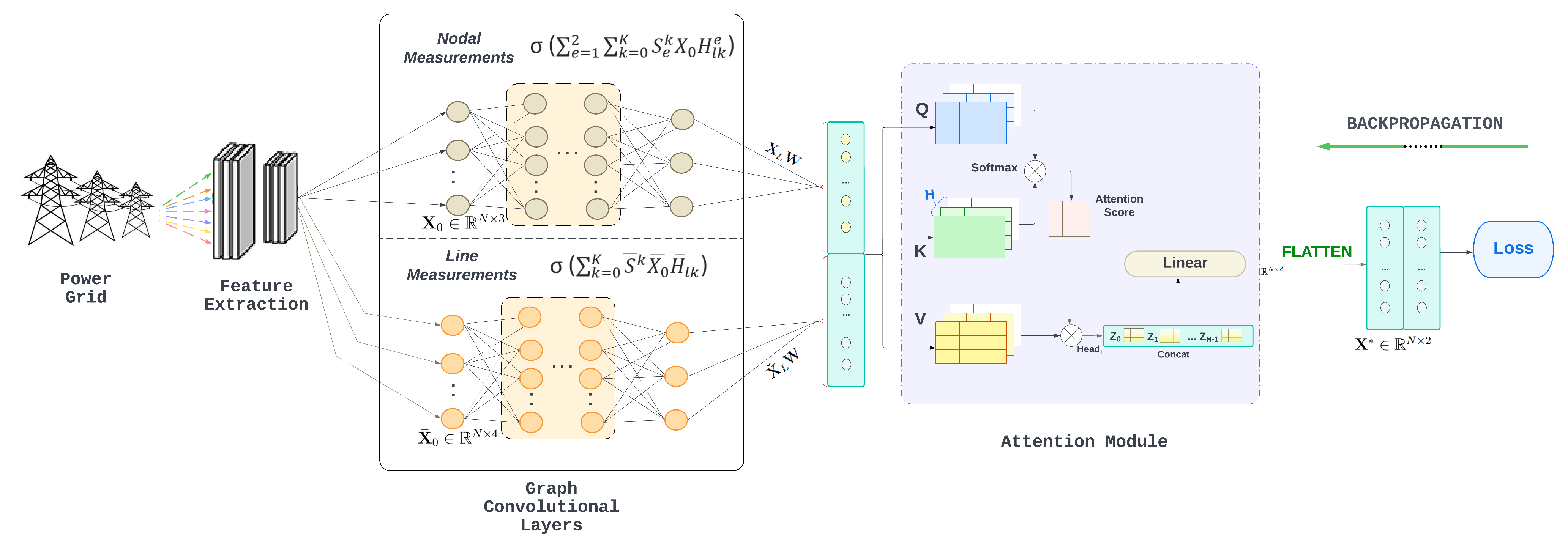
With the increase of data in modern environmental and industrial systems, the ability to extract reliable knowledge from abundant but untrusted data has become more and more important. Various applications in the realm of power grids, socio-economic systems, recommender systems and robotics to name a few, can be characterized by an interconnected network appended by an information layer. However, the information available is often irregular and of complex nature, posing challenges for data analytic tools. For instance, power system measurements are riddled with noise and bad data, and subject to missing values and cyber-attacks. Furthermore, due to laws of physics, the measurement values are nonconvex functions of voltages which limit the application of traditional convex optimization techniques that enjoy strong theoretical and performance guarantees. Nonconvex optimization and learning methods provide two avenues for addressing this issue.

Project 2. Making safe and economic decisions under uncertainty using reliable and scalable computational methods

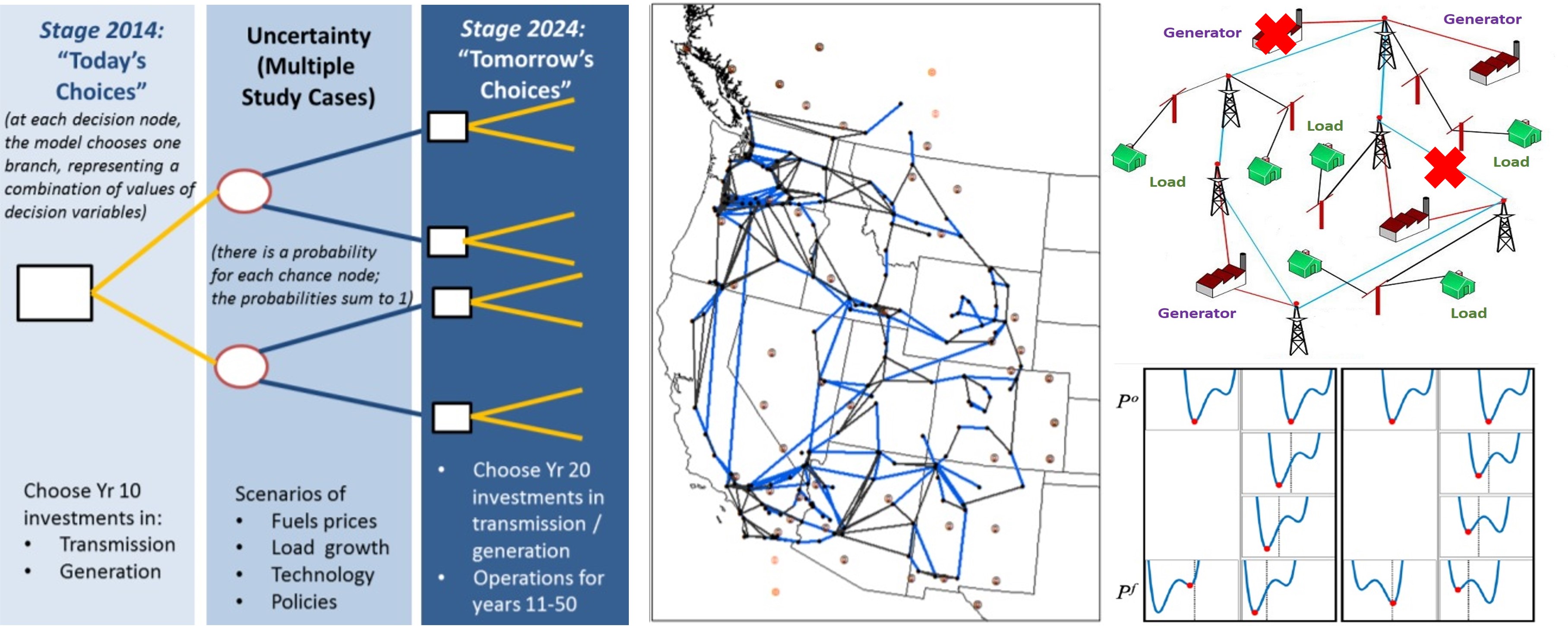
A large number of problems in engineering design, production planning and scheduling, facility location and transportation, resource allocation in finance, and chemical systems require the consideration of uncertainty when making decisions. Without incorporating uncertainty, a deterministic model will perform well under the predicted scenario but may be costly and detrimental when other scenarios unfold. A major challenge in optimization under uncertainty is in coping with an uncertainty space that is enormous, which often adds to the complexity of solving already large-scale optimization problems. These issues are further complicated by the multi-stage nature of many of these problems and by the presence of integer decision variables that model discrete decisions.

Project 3. Safeguarding Electric Power Grids Against Cyber-physical Attacks

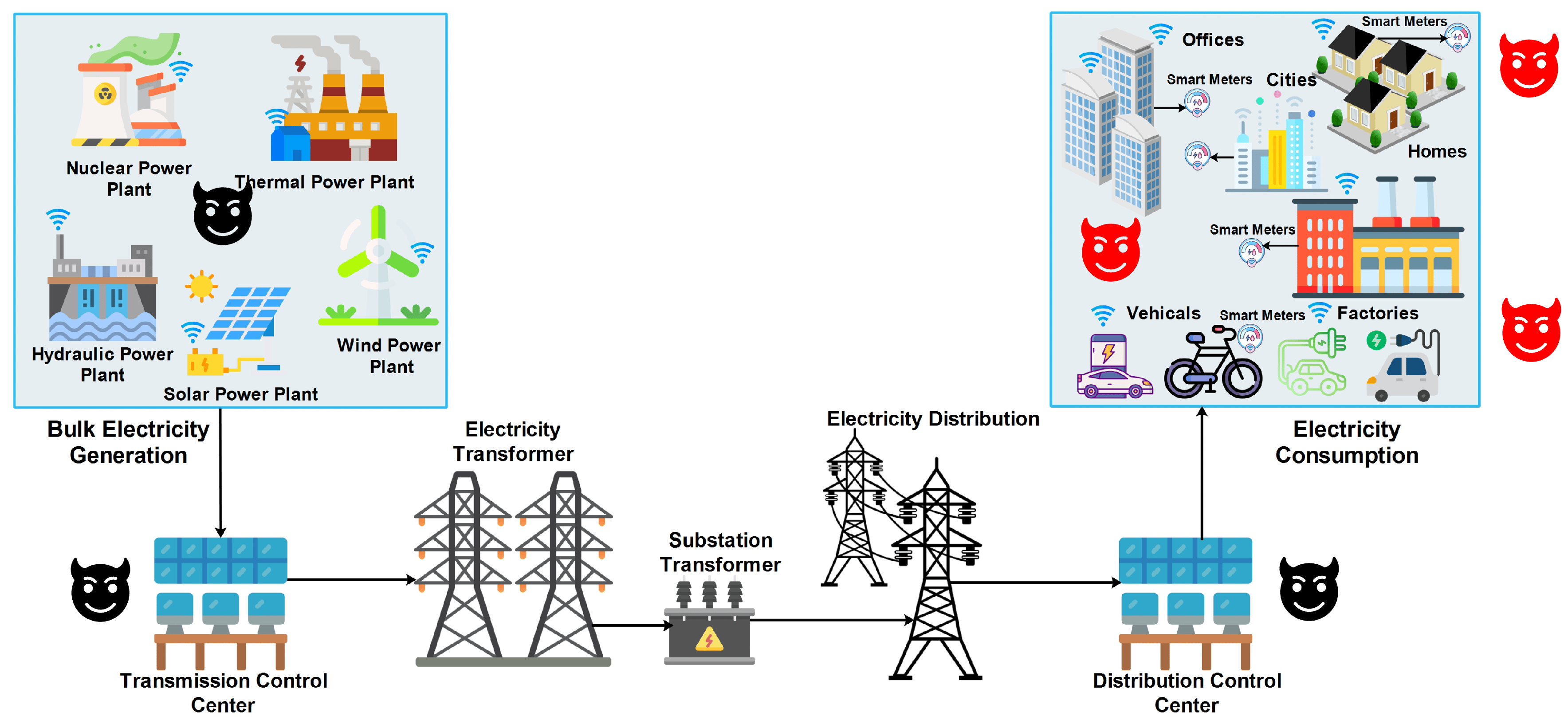
In the future smart grid, almost all devices that generate or consume electricity are integrated into the grid through power electronic interfaces and connected via internet. This drastically increases the cyber-attack surfaces in the grid. Currently, cyber threats are not studied on realistic grid setups   and attack scenarios are not comprehensively explored. We aim to achieve real-time power system security and protection by understanding the stability boundary of power grids with high renewable penetration and designing methodologies for detecting/mitigating cyber-phsyical threats. Advanced computational tools that can deal with transient analyses in addition to steady-state analyses will be developed.